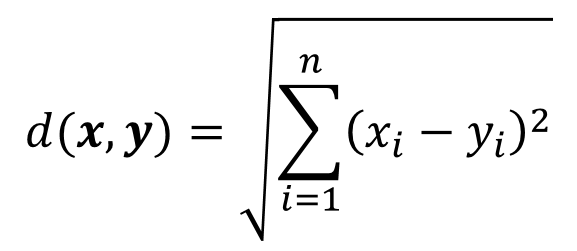神奇的HyperLogLog算法

基数计数基本概念

基数计数(cardinality counting)通常用来统计一个集合中不重复的元素个数，例如统计某个网站的UV，或者用户搜索网站的关键词数量。数据分析、网络监控及数据库优化等领域都会涉及到基数计数的需求。要实现基数计数，最简单的做法是记录集合中所有不重复的元素集合

S_u

Su，当新来一个元素

x_i

$x i$ ，若

S_u

$S u$ 中不包含元素

x_i

$x i$ ，则将

x_i

$x i$ 加入

S_u

$S u$ ，否则不加入，计数值就是

S_u

$S u$ 的元素数量。这种做法存在两个问题：

当统计的数据量变大时，相应的存储内存也会线性增长
当集合
$S_u$
$S u$ 变大，判断其是否包含新加入元素
$x_i$
$x i$ 的成本变大

大数据量背景下，要实现基数计数，首先需要确定存储统计数据的方案，以及如何根据存储的数据计算基数值；另外还有一些场景下需要融合多个独立统计的基数值，例如对一个网站分别统计了三天的UV，现在需要知道这三天的UV总量是多少，怎么融合多个统计值。

B树

B树最大的优势是插入和查找效率很高，如果用B树存储要统计的数据，可以快速判断新来的数据是否已经存在，并快速将元素插入B树。要计算基数值，只需要计算B树的节点个数。将B树结构维护到内存中，可以快速统计和计算，但依然存在问题，B树结构只是加快了查找和插入效率，并没有节省存储内存。例如要同时统计几万个链接的UV，每个链接的访问量都很大，如果把这些数据都维护到内存中，实在是够呛。

bitmap

bitmap可以理解为通过一个bit数组来存储特定数据的一种数据结构，每一个bit位都能独立包含信息，bit是数据的最小存储单位，因此能大量节省空间，也可以将整个bit数据一次性load到内存计算。如果定义一个很大的bit数组，基数统计中每一个元素对应到bit数组的其中一位，例如bit数组

001101001

$001101001$ 代表实际数组

[2,3,5,8]

$[2, 3, 5, 8]$ 。新加入一个元素，只需要将已有的bit数组和新加入的数字做按位或

(or)

$(o r)$ 计算。bitmap中1的数量就是集合的基数值。

bitmap有一个很明显的优势是可以轻松合并多个统计结果，只需要对多个结果求异或就可以。也可以大大减少存储内存，可以做个简单的计算，如果要统计1亿个数据的基数值，大约需要内存： 100000000/8/1024/1024

\approx

$\approx$ 12M
如果用32bit的int代表每个统计数据，大约需要内存：
32*100000000/8/1024/1024

\approx

$\approx$ 381M

bitmap对于内存的节约量是显而易见的，但还是不够。统计一个对象的基数值需要12M，如果统计10000个对象，就需要将近120G了，同样不能广泛用于大数据场景。

概率算法

实际上目前还没有发现更好的在大数据场景中准确计算基数的高效算法，因此在不追求绝对准确的情况下，使用概率算法算是一个不错的解决方案。概率算法不直接存储数据集合本身，通过一定的概率统计方法预估基数值，这种方法可以大大节省内存，同时保证误差控制在一定范围内。目前用于基数计数的概率算法包括:

Linear Counting(LC)：早期的基数估计算法，LC在空间复杂度方面并不算优秀，实际上LC的空间复杂度与上文中简单bitmap方法是一样的（但是有个常数项级别的降低），都是
$O(N_{max})$
$O (N m a x)$ ；
LogLog Counting(LLC)：LogLog Counting相比于LC更加节省内存，空间复杂度只有
$O(log_2(log_2(N_{max})))$
$O (l o g 2 (l o g 2 (N m a x)))$
HyperLogLog Counting(HLL)：HyperLogLog Counting是基于LLC的优化和改进，在同样空间复杂度情况下，能够比LLC的基数估计误差更小。

下面将着重讲HLL的原理和计算过程。

HyperLogLog的惊人表现

上面我们计算过用bitmap存储1一亿个统计数据大概需要12M内存；而在HLL中，只需要不到1K内存就能做到；redis中实现的HyperLogLog，只需要12K内存，在标准误差0.81%的前提下，能够统计

2^{64}

$264$ 个数据。首先容我感叹一下数学的强大和魅力，那么概率算法是怎样做到如此节省内存的，又是怎样控制误差的呢？

首先简单展示一下HLL的基本做法，HLL中实际存储的是一个长度为

m

$m$ 的大数组

S

$S$ ，将待统计的数据集合划分成

m

$m$ 组，每组根据算法记录一个统计值存入数组中。数组的大小

m

$m$ 由算法实现方自己确定，redis中这个数组的大小是16834，

m

$m$ 越大，基数统计的误差越小，但需要的内存空间也越大。

这里有个HLL demo可以看一下HLL到底是怎么做到这种超乎想象的事情的。

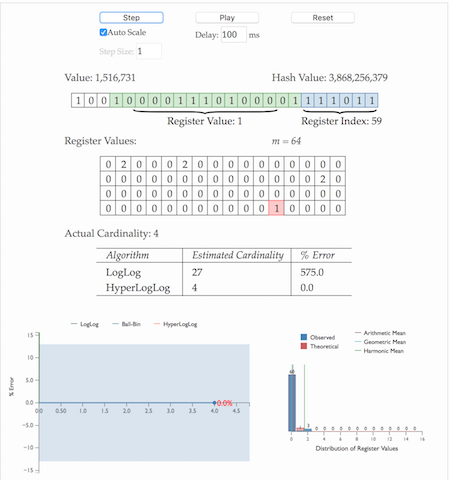
hyperloglog

通过hash函数计算输入值对应的比特串
比特串的低
$t(t=log_2^m)$
$t (t = l o g 2 m)$ 位对应的数字用来找到数组
$S$
$S$ 中对应的位置
$i$
$i$
$t+1$
$t + 1$ 位开始找到第一个1出现的位置
$k$
$k$ ，将
$k$
$k$ 记入数组
$S_i$
$S i$ 位置
基于数组
$S$
$S$ 记录的所有数据的统计值，计算整体的基数值，计算公式可以简单表示为：
$\hat{n}=f(S)$
$n^= f (S)$

看到这里心里应该有无数个问号，这样真的就能统计到上亿条数据的基数了吗？我总结一下，先抛出三个疑问：

为什么要记录第一个1出现的位置？
为什么要有分桶数组
$S$
$S$ ？
通过分桶数组
$S$
$S$ 计算基数的公式是什么？

hyperloglog原理理解

举一个我们最熟悉的抛硬币例子，出现正反面的概率都是1/2，一直抛硬币直到出现正面，记录下投掷次数

k

$k$ ，将这种抛硬币多次直到出现正面的过程记为一次伯努利过程，对于

n

$n$ 次伯努利过程，我们会得到

n

$n$ 个出现正面的投掷次数值

k_1

$k 1$ ,

k_2

$k 2$ ……

k_n

$k n$ ，其中最大值记为

k_{max}

$k m a x$ ，那么可以得到下面结论：

$n$
$n$ 次伯努利过程的投掷次数都不大于
$k_{max}$
$k m a x$
$n$
$n$ 次伯努利过程，至少有一次投掷次数等于
$k_{max}$
$k m a x$

对于第一个结论，

n

$n$ 次伯努利过程的抛掷次数都不大于

k_{max}

$k m a x$ 的概率用数学公式表示为：

P_n(X \le k_{max})=(1-1/2^{k_{max}})^n

$P n (X \leq k m a x) = (1 - 1 / 2 k m a x) n$

第二个结论至少有一次等于

k_{max}

$k m a x$ 的概率用数学公式表示为：

P_n(X \ge k_{max})=1-(1-1/2^{k_{max}-1})^n

$P n (X \geq k m a x) = 1 - (1 - 1 / 2 k m a x - 1) n$

当

n\ll 2^{k_{max}}

$n ≪ 2 k m a x$ 时，

P_n(X \ge k_{max})\approx0

$P n (X \geq k m a x) \approx 0$ ，即当

n

$n$ 远小于

2^{k_{max}}

$2 k m a x$ 时，上述第一条结论不成立；
当

n\gg 2^{k_{max}}

$n ≫ 2 k m a x$ 时，

P_n(X \le k_{max})\approx0

$P n (X \leq k m a x) \approx 0$ ，即当

n

$n$ 远大于

2^{k_{max}}

$2 k m a x$ 时，上述第二条结论不成立。因此，我们似乎就可以用

2^{k_{max}}

$2 k m a x$ 的值来估计

n

$n$ 的大小。

以上结论可以总结为：进行了

n

$n$ 次进行抛硬币实验，每次分别记录下第一次抛到正面的抛掷次数

k

$k$ ，那么可以用n次实验中最大的抛掷次数

k_{max}

$k m a x$ 来预估实验组数量

n

$n$ ：

\hat{n} = 2^{k_{max}}

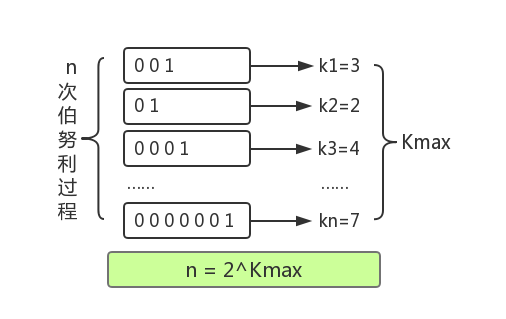$n^= 2 k m a x$ 原型图 (1).png-18.1kB 可以通过一组小实验验证一下这种估计方法是否基本合理。

回到基数统计的问题，我们需要统计一组数据中不重复元素的个数，集合中每个元素的经过hash函数后可以表示成0和1构成的二进制数串，一个二进制串可以类比为一次抛硬币实验，1是抛到正面，0是反面。二进制串中从低位开始第一个1出现的位置可以理解为抛硬币试验中第一次出现正面的抛掷次数

k

$k$ ，那么基于上面的结论，我们可以通过多次抛硬币实验的最大抛到正面的次数来预估总共进行了多少次实验，同样可以可以通过第一个1出现位置的最大值

k_{max}

$k m a x$ 来预估总共有多少个不同的数字（整体基数）。

这种通过局部信息预估整体数据流特性的方法似乎有些超出我们的基本认知，需要用概率和统计的方法才能推导和验证这种关联关系。HyperLogLog核心在于观察集合中每个数字对应的比特串，通过统计和记录比特串中最大的出现1的位置来估计集合整体的基数，可以大大减少内存耗费。

现在回到第二节中关于HyperLogLog的第一个疑问，为什么要统计hash值中第一个1出现的位置？
第一个1出现的位置可以类比为抛硬币实验中第一次抛到正面的抛掷次数，根据抛硬币实验的结论，记录每个数据的第一个出现的位置

k

$k$ ，就可以通过其中最大值

{k_{max}}

$k m a x$ 推导出数据集合的基数：

\hat{n} = 2^{k_{max}}

$n^= 2 k m a x$ 。

hyperloglog算法讲解

分桶平均

HLL的基本思想是利用集合中数字的比特串第一个1出现位置的最大值来预估整体基数，但是这种预估方法存在较大误差，为了改善误差情况，HLL中引入分桶平均的概念。
同样举抛硬币的例子，如果只有一组抛硬币实验，运气较好，第一次实验过程就抛了10次才第一次抛到正面，显然根据公式推导得到的实验次数的估计误差较大；如果100个组同时进行抛硬币实验，同时运气这么好的概率就很低了，每组分别进行多次抛硬币实验，并上报各自实验过程中抛到正面的抛掷次数的最大值，就能根据100组的平均值预估整体的实验次数了。

分桶平均的基本原理是将统计数据划分为

m

$m$ 个桶，每个桶分别统计各自的

{k_{max}}

$k m a x$ 并能得到各自的基数预估值

\hat{n}

$n^$ ，最终对这些

\hat{n}

$n^$ 求平均得到整体的基数估计值。LLC中使用几何平均数预估整体的基数值，但是当统计数据量较小时误差较大；HLL在LLC基础上做了改进，采用调和平均数，调和平均数的优点是可以过滤掉不健康的统计值，具体的计算公式为：

回到第二节中关于HLL的第二个疑问，为什么要有分桶数组？分桶数组是为了消减因偶然性带来的误差，提高预估的准确性。那么分桶数组的大小怎么确定呢？
这是由算法实现方自己设定的，例如上面HLL demo中，设定统计数组的大小，如果函数得到的比特串是32位，需要其中6()位定位分桶数组中的桶的位置，还剩下26位（需要记录的出现1的位置的最大值是26），那么数组中每个桶需要5()位记录1第一次出现的位置，整个统计数组需要花费的内存为：

也就是用32bit的内存能够统计的基数数量为。

偏差修正

上述经过分桶平均后的估计量看似已经很不错了，不过通过数学分析可以知道这并不是基数n的无偏估计。因此需要修正成无偏估计。这部分的具体数学分析在“Loglog Counting of Large Cardinalities”中。

其中系数由统计数组的大小决定，具体的公式为：

根据论文中分析结论，HLL与LLC一样是渐进无偏估计，渐进标准误差表示为：

因此，统计数组大小越大，基数统计的标准误差越小，但需要的存储空间也越大，在的情况下，HLL的标准误差为1.1%。

虽然调和平均数能够适当修正算法误差，但作者给出一种分阶段修正算法。当HLL算法开始统计数据时，统计数组中大部分位置都是空数据，并且需要一段时间才能填满数组，这种阶段引入一种小范围修正方法；当HLL算法中统计数组已满的时候，需要统计的数据基数很大，这时候hash空间会出现很多碰撞情况，这种阶段引入一种大范围修正方法。最终算法用伪代码可以表示为如下。

m = 2^b   # with b in [4...16]if m == 16:
    alpha = 0.673elif m == 32:
    alpha = 0.697elif m == 64:
    alpha = 0.709else:
    alpha = 0.7213/(1 + 1.079/m)registers = [0]*m   # initialize m registers to 0############################################################################ Construct the HLL structurefor h in hashed(data):
    register_index = 1 + get_register_index( h,b ) # binary address of the rightmost b bits
    run_length = run_of_zeros( h,b ) # length of the run of zeroes starting at bit b+1
    registers[ register_index ] = max( registers[ register_index ], run_length )########################################################################### Determine the cardinalityDV_est = alpha * m^2 * 1/sum( 2^ -register )  # the DV estimateif DV_est < 5/2 * m: # small range correction
    V = count_of_zero_registers( registers ) # the number of registers equal to zero
    if V == 0:  # if none of the registers are empty, use the HLL estimate
          DV = DV_est
    else:
          DV = m * log(m/V)  # i.e. balls and bins correctionif DV_est <= ( 1/30 * 2^32 ):  # intermediate range, no correction
     DV = DV_estif DV_est > ( 1/30 * 2^32 ):  # large range correction
     DV = -2^32 * log( 1 - DV_est/2^32)

redis中hyperloglog实现

redis正是基于以上的HLL算法实现的HyperLogLog结构，用于统计一组数据集合中不重复的数据个数。 redis中统计数组大小设置为，hash函数生成64位bit数组，其中位用来找到统计数组的位置，剩下50位用来记录第一个1出现的位置，最大位置为50，需要位记录。

那么统计数组需要的最大内存大小为：基数估计的标准误差为。可以学习一下redis中HyperLogLog的源码实现。

参考阅读
Redis new data structure: the HyperLogLog
HyperLogLog — Cornerstone of a Big Data Infrastructure
解读Cardinality Estimation算法（第四部分：HyperLogLog Counting及Adaptive Counting）

转载请注明：学时网 » 神奇的HyperLogLog算法

学时网 -关注编程生活文学，分享智慧与快乐

神奇的HyperLogLog算法

基数计数基本概念

B树

bitmap

概率算法

HyperLogLog的惊人表现

hyperloglog原理理解

hyperloglog算法讲解

分桶平均

偏差修正

redis中hyperloglog实现

相似文章

您必须登录才能发表评论！

2025年 5月
一	二	三	四	五	六	日
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30

基数计数基本概念

B树

bitmap

概率算法

HyperLogLog的惊人表现

hyperloglog原理理解

hyperloglog算法讲解

分桶平均

偏差修正

redis中hyperloglog实现

相似文章

您必须 登录 才能发表评论！

您必须登录才能发表评论！